1 工程概述
上海国际旅游度假区空间曲梁单边悬索桥东桥跨径组合为“43.60 m+80.00 m+43.60 m”,西桥跨径组合为“28.20 m+48.20 m+28.20 m”,2座桥设计结构基本相同。
东、西桥拉索均为锌-5%铝-混合稀土合金镀层密封钢索,吊索直径包含38 mm和63 mm两种规格,其中与主塔连接的吊索直径规格为63 mm,其余各吊索直径规格均为38 mm。东桥的背索规格为φ115 mm,西桥的背索规格为φ90 mm。东桥背索如图1所示,东桥主吊索(主塔处吊索)如图2所示。
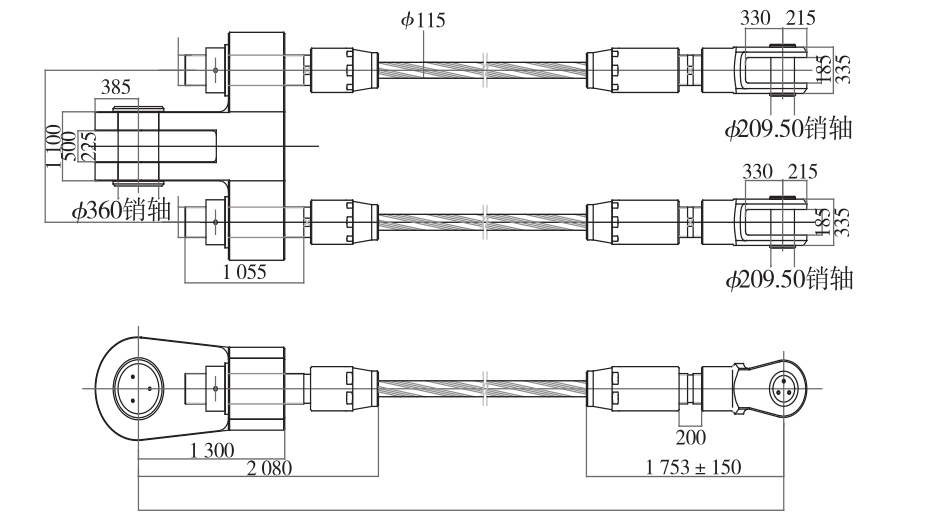
图1 东桥背索结构示意
由东西两桥背索和主吊索的详图可知,背索和吊索两端均近似铰接,索长取两铰中心之间的距离,其中东桥吊索长度范围为2.45~20.72 m,西桥吊索长度范围为2.56~13.74 m,特别短的索只能保证基频测量的精度,基频换算为索力的计算公式误差较大。
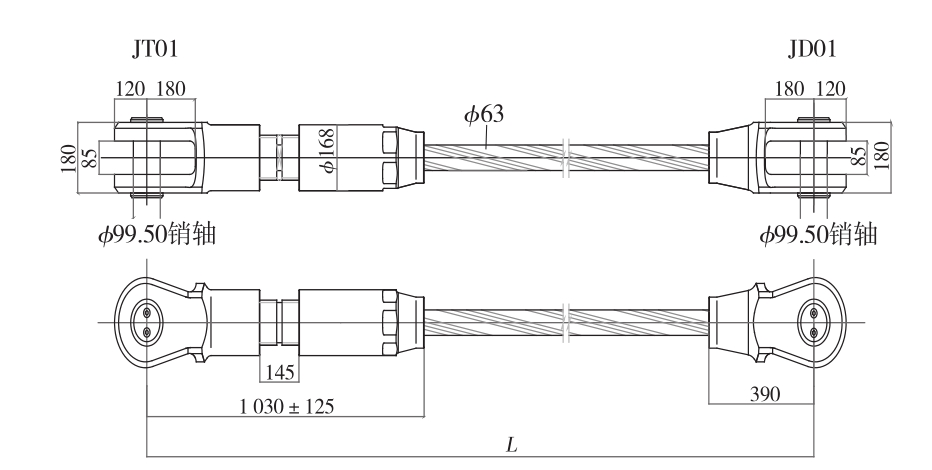
图2 东桥主吊索结构示意
2 荷载试验目的及内容
2.1 试验目的
桥梁静力荷载试验,主要是通过测量桥梁结构在静力试验荷载作用下的变形和内力,用以确定桥梁结构的实际工作状态与设计期望值是否相符。它是检验桥梁结构实际工作性能最直接和最有效的手段和方法。
本试验旨在通过测量背索索力、吊索索力来反映桥梁的实际工作状态,并判断吊索和背索的安全储备。
2.2 测试工况
为了保证加载过程中结构的安全和测试的完整性,东西两桥均按照以下工况加载和卸载:初始值,主桥空载、副桥半载,主桥空载、副桥满载,主桥半载、副桥满载,主桥满载、副桥满载,偏载,主桥满载、副桥空载,卸载后。为了验证本文的2种基频推算索力的计算方法,选取索力变化较大的工况进行数据分析,如表1所示。
表1 东西桥索力分析工况
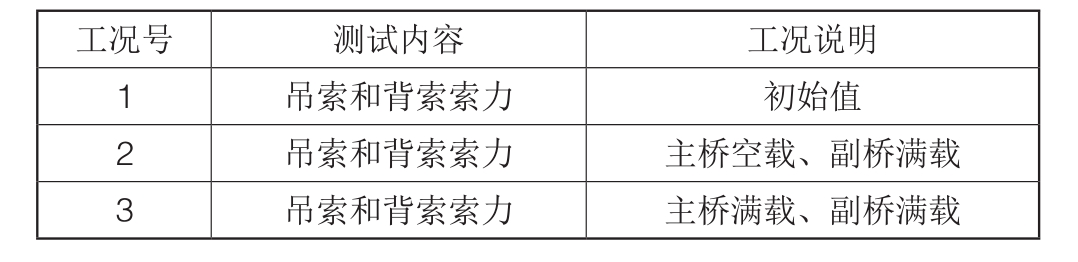
工况号 测试内容 工况说明1吊索和背索索力 初始值2吊索和背索索力 主桥空载、副桥满载3吊索和背索索力 主桥满载、副桥满载
3 刚性索测试方法
3.1 测试流程
利用频率法测试索力的现场流程为:绑扎加速度传感器→信号采集仪调试→采样频率选择→采样→滤波→信号分析→计算处理。
绑扎加速度传感器需要注意的是距离锚固端减振器距离应大于1.50 m,在现场条件允许的情况下宜远离锚固端;且传感器的敏感方向宜与拉索较易发生的横向振动方向一致。
信号采集仪的调试主要指基线漂移处理,结构的温度变化或者低阶振动均有可能造成信号零基准点的漂移,漂移的过程是连续变化的,使得监测信号在整个采集过程中均产生误差,所以在采集之前应进行基线漂移处理[1-2]。
根据采样定理和工程实践,一般情况要求采样频率至少为被测信号的2.5倍;采用频率的选择视关拉索的频率的阶数而定,在采样之前可以根据式(1)估算拉索基频,而采样频率取估算基频的6~8倍。

式中:Tq——期望索力,N;
L——拉索的计算长度,m;
m——拉索单位长度的质量,kg/m。
滤波是将噪声滤去,并将信号进行一定程度放大,在进行信号采集时,应用低通滤波器将高于分析频率的信号滤掉,以免频率混叠的发生。
信号分析指的是将信号数字化,然后通过FFT变换得出功率谱图,在实践中要注意的是FFT分析的点数的选择,过低造成分析的精度不够,过高则要求采样的块数较多,不利于快速取样。最后的计算处理则是根据频率和索力的对应关系,将频率值换算成索力值。
3.2 2种换算方法
利用频率法测试索力的精度主要取决于2方面:一是拉索频率的测试精度,主要体现在频率识别的问题;二是索力分析计算方法的精度,对于拉索两端边界条件可以简化成铰支的刚性索,可采用公式法推算索力。方法一是根据弦的振动理论,对于张紧的索,当忽略其垂度影响时,在无阻尼时的自由振动方程如式(2)所示:
运用分离变量法对上述公式进行求解,在拉索两端为铰接的边界条件下,可以得到拉索索力和振动频率的关系如式(3)所示:
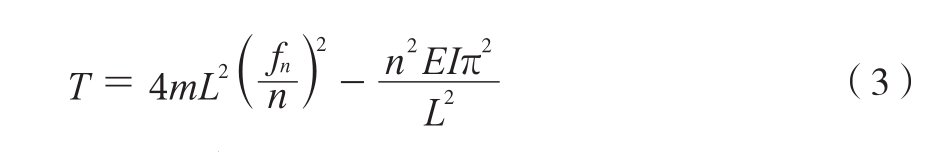
式中:T——索力,N;
n——索自振频率的阶数;
fn——第n阶自振频率;
L——拉索的计算长度,m;
I——拉索截面刚度,可取与全断面钢丝面积相等的
圆截面惯性矩,m4。
由于截面刚度难以确定其真实值,所以方法二是采用抵消截面刚度的方法。对于可以将拉索两端简化成铰支边界条件的情况,又能测得二阶以上的拉索振动频率,则可以根据测得的任意两阶频率计算索力如式(4)所示:
式中:fn——实测的第n阶拉索振动频率;
fc1——只考虑几何刚度时的索的第1阶振动频率;
fb1——只考虑弯曲刚度时的索的第1阶振动频率。分别将任意两阶拉索的实测振动频率代入上式消去fb1即可得到fc1,再利用公式T=4 mfc1 2L2计算索力,这样得到的索力即消除了抗弯刚度对频率的影响。
3.3 拉索计算参数的确定
换算公式确定以后,需根据公式确定拉索的计算参数。因为本工程各拉索的索长均较短,且为刚性索,所以拉索计算参数还应包括拉索的质量、弹性模量、截面抗弯刚度等参数。
拉索的质量根据图纸信息获取,方法一中用到的截面抗弯刚度按照拉索的规格进行面积相等的圆截面惯性矩换算。拉索的弹性模量则通过实测获取。测量所得的各种规格拉索的弹性模量如表2所示。
表2 各规格拉索弹性模量实测值
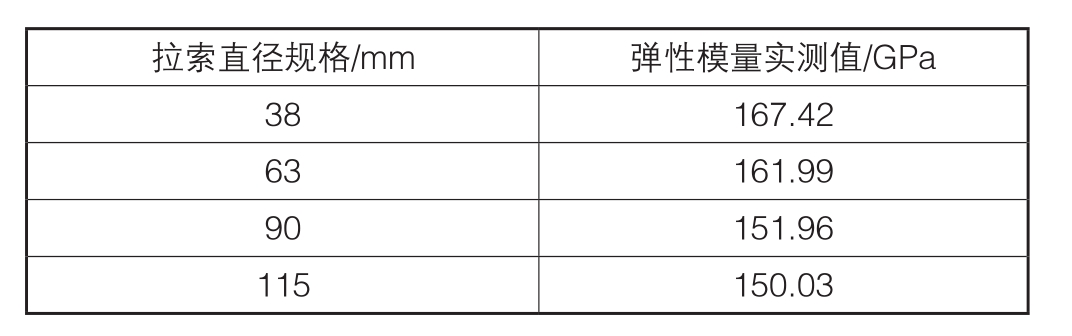
拉索直径规格/mm 弹性模量实测值/GPa 38 167.42 63 161.99 90 151.96 115 150.03
3.4 换算结果分析
在实测过程中,为了排除温度的影响,本荷载试验各工况各拉索索力的测量时间均控制在清晨03:30~06:30,结构温度在26~28℃,荷载加载过程由监理单位进行监督检查,因此满足各项荷载试验条件,测量数据受加载及温度影响相对较小。图3展示的是典型的频谱分析结果。
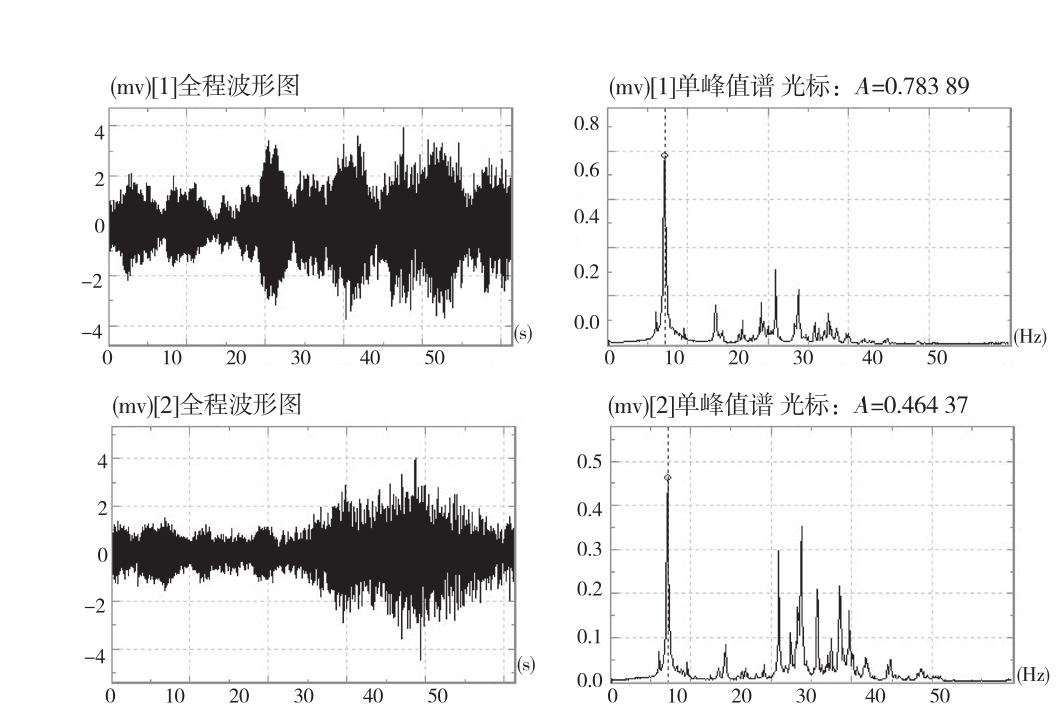
图3 典型索力测试频谱分析
根据东西桥测得的频率值分别用方法一和方法二进行索力值的换算,其中方法一采用基频值计算,方法二采用基频值和二阶频率值进行换算。
为了比较2种方法的换算效果,将方法一和方法二的实测增量值和理论增量值的偏差用“方法一偏差”和“方法二偏差”表示,分别进行计算,计算结果见图4、图5。
由分析可知,运用2种方法换算的索力实测增量值和理论增量值的偏差的趋势基本是一致的。
对于东桥,工况一到工况二的增量偏差分析中,方法一和方法二换算的吊索偏差绝对值最大分别为33.90 kN和32.70 kN,背索偏差绝对值最大分别为53.30 kN和34.50 kN;工况二到工况三的增量偏差分析中,方法一和方法二换算的吊索偏差绝对值最大分别为87.60 kN和85.50 kN,背索偏差绝对值最大分别为169.00 kN和192.20 kN。
对于西桥,工况一到工况二的增量偏差分析中,方法一和方法二换算的吊索偏差绝对值最大分别为47.70 kN和49.40 kN,背索偏差绝对值最大分别为26.10 kN和31.80 kN;工况二到工况三的增量偏差分析中,方法一和方法二换算的吊索偏差绝对值最大分别为32.10 kN和30.10 kN,背索偏差绝对值最大分别为44.40 kN和66.90 kN。
分析可知,偏差绝对值较大的拉索基本为背索和主塔对应处的主吊索,这是因为背索和主吊索的索力绝对值都较大[3-4]。
4 结语
由本荷载试验索力测量的实践可知:
1)索力测试的精度既取决于拉索频率的测试精度,也取决于索力换算方法的精度。
2)在索力测试过程中应注意信号零基准点的漂移、采用频率的选取等问题。
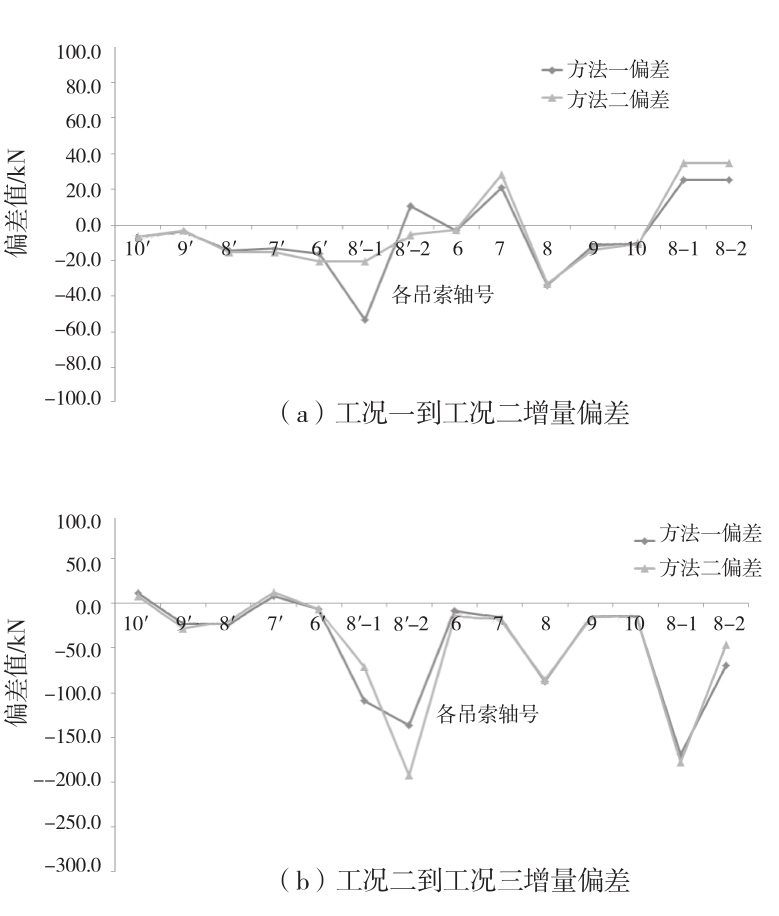
图4 东桥增量偏差分析
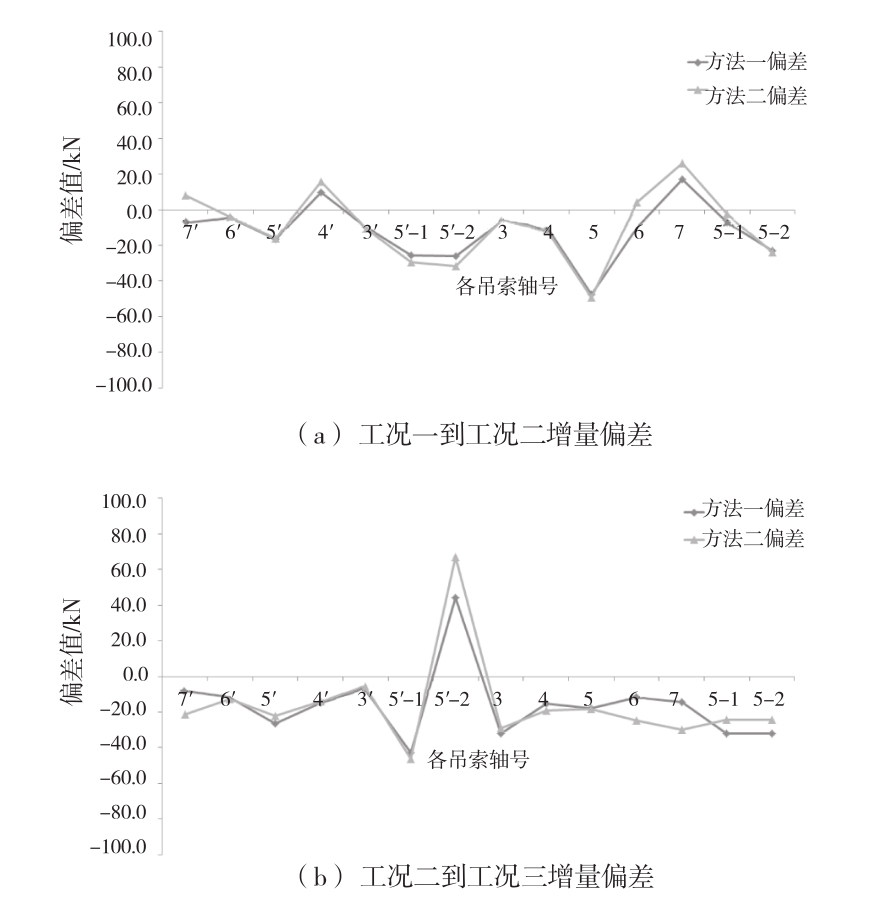
图5 西桥增量偏差分析
3)对于短索,不能忽视索抗弯刚度对于索力换算的影响,文中提到的2种方法均可以修正索的抗弯刚度的影响。公式计算方便简单,可供工程实际应用,误差在工程允许范围之内。
[1] 吴康雄,刘克明,杨金喜.基于频率法的索力测量系统[J].中国公路学报,2006(2):62-66.
[2] 任伟新,陈刚.由基频计算拉索拉力的实用公式[J].土木工程学报,2005(11):26-31.
[3] 郝超,裴岷山,强士中.斜拉桥索力测试新方法:磁通量法[J].公路,2000(11):30-31.
[4] 王红平.斜拉索索力监测技术研究与应用[D].西安:长安大学,2002.